The area of a convex polygon from the coordinates of the vertices on the plane
This online calculator calculates the area of a convex polygon from the coordinates of the vertices. A convex polygon is built from the vertices using the Jarvis March Algorithm (or Gift Wrapping Algorithm)
The calculator below was written to solve a particular problem of calculating the area of a convex quadrilateral from the coordinates of its vertices. It generalizes this problem to the problem of calculating the area of any convex polygon. The site already has a similar calculator Polygon area, but there you need to enter the lengths of the sides and diagonals, and this is somewhat more difficult than entering only the coordinates of the vertices.
How to use the calculator: start entering the coordinates of the vertices of the convex polygon. Starting from third point, the Jarvis algorithm will build a convex hull, then we break the hull into triangles and calculate the total area. For reference, the areas of all triangles will also be displayed.
You can read about the inner details of calculation below the calculator.
The area of a convex polygon from the coordinates of the vertices on the plane
Polygon vertices
| Point | X | Y | ||
|---|---|---|---|---|
Convex Hull and Jarvis March
The idea is simple - the polygon is divided into non-intersecting triangles, the area of all triangles is calculated (this is easy to do knowing the lengths of all three sides - Heron's formula calculator), then the areas are summed up. The main problem was to make it resistant to the situation when the vertices are entered out of order. Suppose the first four points are entered to get the shape in the figure below
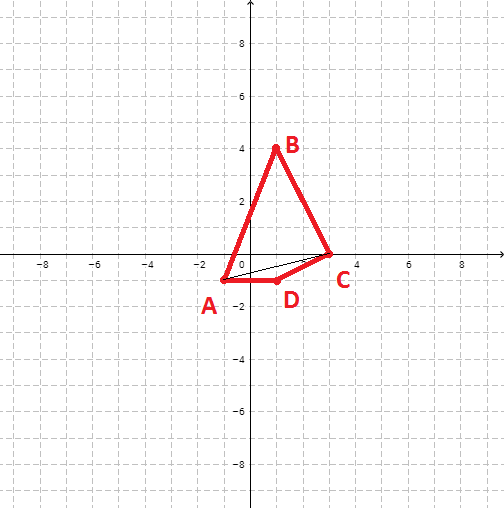
When adding the next point, for example, as in the following figure
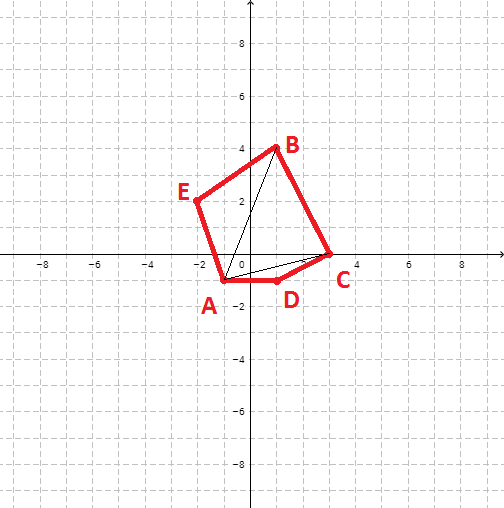
we should obtain the polygon ADCBE, not ABCDE, broken into triangles ADC, ACB and ABE, respectively.
To get a convex polygon, you actually need to get the convex hull of the entered points. To do this, the calculator uses Gift wrapping algorithm (or Jarvis march). The method can be imagined as wrapping a set of nails hammered into a board with a rope.
The algorithm runs in time, where n is the total number of points on the plane, h is the number of points in the convex hull. For a convex polygon, respectively, it will be
. Not the most optimal algorithm, but very simple, and quite productive for this calculator.
Comments