Conversion between Gauss planar rectangular coordinates and geographic coordinates and vice versa
The page contains online calculators for converting from geographic coordinates to Gauss planar rectangular coordinates and back (the formulas for the Krasovsky reference ellipsoid are used).
The flat rectangular Gaussian coordinates x and y are related to the geographic coordinates φ (latitude) and λ (longitude) of points on the Earth's surface by rather complicated formulas (transformation keys). Below are two calculators that make the conversion from one coordinate to the other.
These calculators use transformation keys calculated for the Krasovsky reference ellipsoid, or SK-42 coordinate system. The use of SK-42 is only allowed until January 1, 2021, so these calculators are more of historical interest.
Geographic coordinates to Gauss-Krueger planar rectangular coordinates converter
Gauss-Kruger planar rectangular coordinates to geographic coordinates converter
Zonal Gauss planar rectangular coordinate system
In topography and geodesy, the use of rectangular coordinates is widespread. Simply because kilometers and meters are easier to use than degrees, minutes and seconds. As a system of planar rectangular coordinates, the Gauss system of planar rectangular coordinates based on the Gauss-Krueger projection is usually used (in 1825-1830 Gauss developed the transverse-cylindrical conformal (equiangular) projection of an ellipsoid on the plane, and Krueger in 1912 derived working formulas of calculations for it).
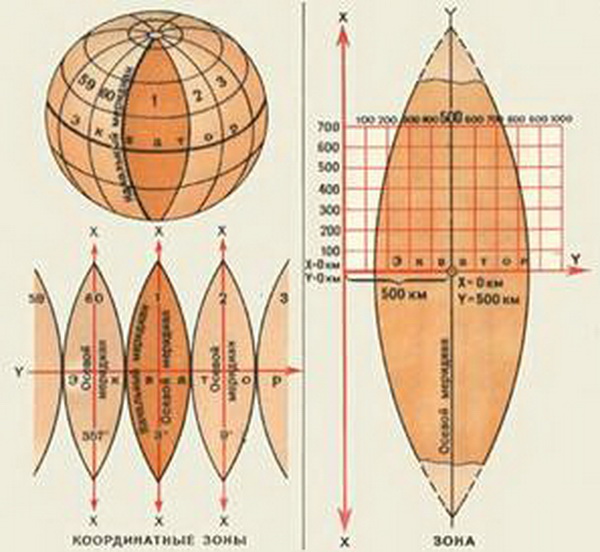
The essence, in brief, is that the Earth ellipsoid is divided by meridians into spherical bi-angles - zones. Then each zone is projected onto the inner side surface of a cylinder, which, by turning it around,
you get a projection of the Earth's surface. Width of a zone - 6 degrees, that is in total there are 60 zones. In Russia zones are counted from the zero meridian (axial meridian of the first zone - 3 degrees of east longitude). Within each zone there is a different coordinate system including the number of the zone. The width of any coordinate zone is approximately 670 km at the equator, 510 km at latitude 40°, and 430 km at latitude 50°. The x-coordinate along the meridian in the northern hemisphere is always positive, to make the y-coordinate positive as well, the origin is shifted 500 km to the left of the axial meridian. See the illustration below (original source of the image is unknown).
Comments