PLANETCALC Online calculators

Login
StudyMathGeometry

Cutting a circle

Two ways to cut a circle into equal parts : sector cuts and parallel cuts.

Below you can find two calculators which calculate how to cut a circle into equal parts - traditional and non-traditional way. By the traditional way, I assume cutting a circle into sectors, just like you usually cut a pie or pizza. And by the non-traditional way, I assume cutting a circle into equal vertical slices with parallel lines or with parallel chords, if you like. Both calculators present a drawing that illustrates the result. And you can find all formulas and math in the article below the calculators.

PLANETCALC, Cutting a Circle into equal sectors

Cutting a Circle into equal sectors

Digits after the decimal point: 2
Angle of a Sector
 
Length of an Arc of a Sector
 
Length of a Chord of a Sector
 

PLANETCALC, Cutting a Circle into equal parts with Parallel Cuts

Cutting a Circle into equal parts with Parallel Cuts

Digits after the decimal point: 2
The file is very large. Browser slowdown may occur during loading and creation.

Cutting a Circle into Sectors

Ok, you need to cut a circle into several sectors (even non-even numbers). To do this, you need to find the parameters of a sector. It is a straightforward task:

  1. Find the angle of a sector in radians by dividing 2π (representing 360 degrees in radians) by a number of sectors.

\alpha=\frac{2\pi}{N}

  1. Find the length of an arc of a sector by multiplying a radius by an angle of a sector in radians.

a=\alpha R

  1. Find the length of a chord of a sector by using Law of cosines (a chord is the base of the isosceles triangle, with two radiuses as legs and sector angle as apex angle).

c=R^2+R^2-2RR \cos \alpha

This completely defines all N equal sectors.

Cutting a Circle with Parallel Cuts

This way is more interesting. For simplicity, I will consider half of a circle since it is symmetrical.

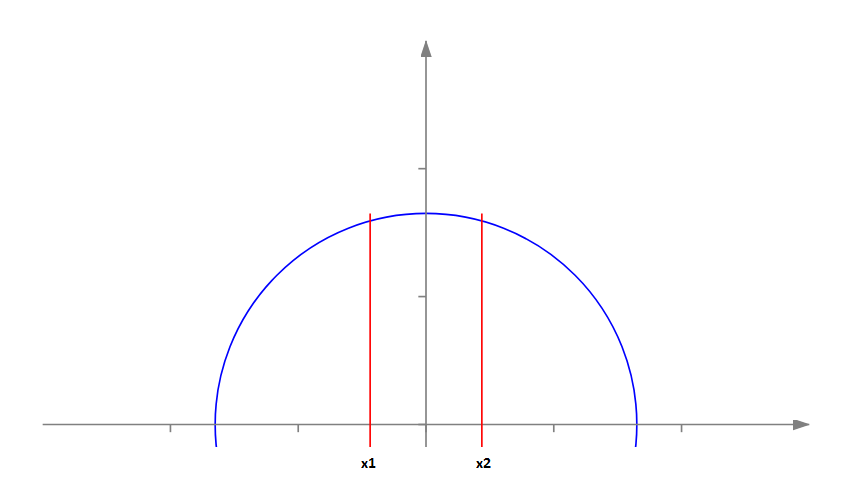
Cutting a Circle into Three Parts with Two Parallel Lines
Cutting a Circle into Three Parts with Two Parallel Lines

Let's slice it with vertical slices. In this case, we need to find the x-coordinates of parallel chords, which should split our circle into equal-area parts. (see points x1 and x2 on the picture above). Let's derive the general formula for an area of a left slice.

Our half-circle can be thought of as a function y=f(x), where x - is the coordinate along the abscissa axis, and y is the function equal to the value of the corresponding half-circle point.

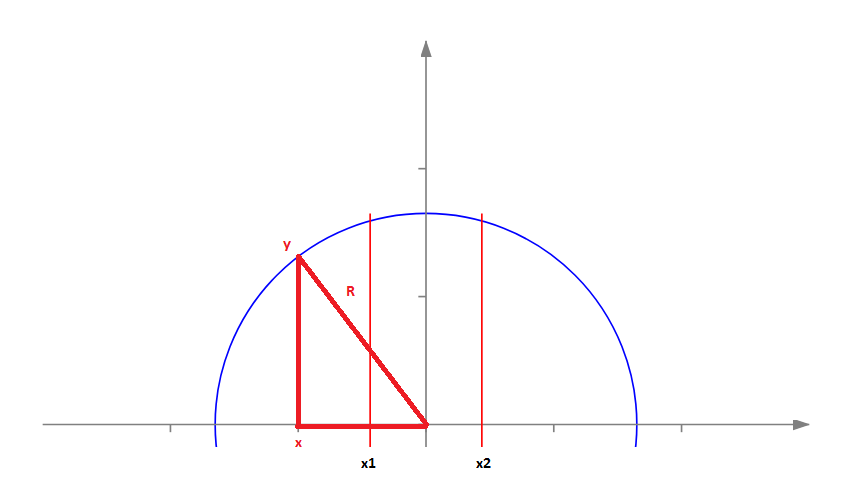
y=f(x)
y=f(x)

Using the Pythagorean theorem, the y function is

y=\sqrt{R^2 - x^2}}

To find an area of a left slice, you need to integrate this function from -R to x. The antiderivative of our function is :

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+C

We need to find the value of constant. Obviously, at the point where x equals -R area should be zero. If we plug -R instead of x into the formula above, we get

F(-R)=-\frac{\pi R^2}{4}+C=0, hence

C=\frac{\pi R^2}{4}

Our final integral is

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}

Now how do we find x of the first cut? We know we area we should get - Nth part of the total area (note the half-circle)

S=\frac{\frac{\pi R^2}{2}}{N}=\frac{\pi R^2}{2N}

Thus we can equate

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}=\frac{\pi R^2}{2N}

Which gives us

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}-\frac{\pi R^2}{2N}=0

This is a transcendental equation, and we need to use numerical methods to solve it, for example, Bisection method or Newton's method. Here I used Newton's method.

The next points of cut can be found with the same approach. We need to cut two times more for second point S_2=2\frac{\pi R^2}{2N}, three times more for third point S_3=3\frac{\pi R^2}{2N} and so on.

Then we can find all other parameters, like chord length, using the point coordinates.

URL copied to clipboard

Similar calculators

 #circle #geometry angle arc area chord circle cut Geometry parallel sector
PLANETCALC, Cutting a circle
Timur2021-03-26 21:32:11

Comments