Volume of the hemisphere cut at an angle
Volume of hemisphere asymmetrically cut by a flat plane under a given angle.
The calculator below gives volume of a body formed by a hemisphere cut by a flat surface under a given angle at a given distance from the hemisphere edge.
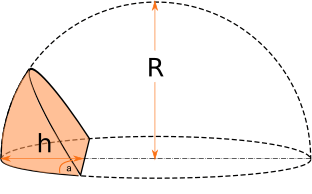
The cut angle is between (0..180) degrees, the height must not exceed the hemisphere diameter. You may find calculation formulas just below the calculator.
Formulas to calculate hemisphere cut volume
Let's start with simple cases.
Hemisphere cut over center h=R
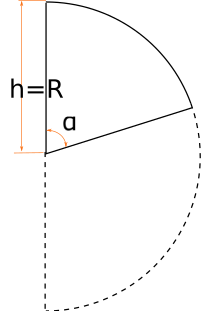
This is simplest case - we just need slightly modify hemisphere volume formula:
In this way:
, where a is the cut angle in radians.
Hemisphere cut under 90 degrees
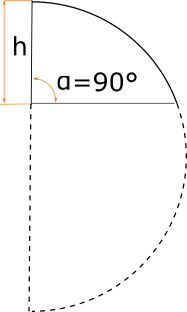
If the hemisphere is cut under right angle, we simply take half spherical cap volume.
Hemisphere cut below center h > R
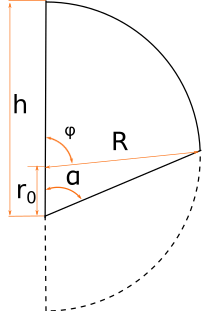
We observe the hardest case when the hemisphere is cut below the center, so remained base edge exceeds the hemisphere radius. In this case we calculate discarded part volume and subtract it from the hemisphere volume to obtain remained part volume:
Vd is calculated by the formulas below, assuming
Hemisphere cut above center h < R
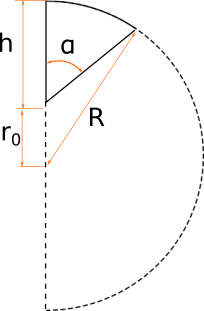
This general case we'll solve by volume integral.
To simplify integration limits we place our hemisphere cut parallel to Z-O-Y plane, so the hemisphere center point is at 0 and the cutting plane is at sin(α)*r0 distance from the Z-O-Y plane (where r0=R-h is a distance from the cutting plane to the hemisphere center):
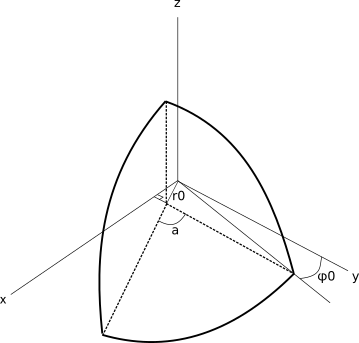
Cutting plane equation in linear coordinate system is .
In spherical (ISO) coordinate system: (1)
Now we solve volume integral for our hemisphere cut in spherical coordinate system:
(2)
We integrate over one hemisphere half, and multiply volume integral by two, since we put the cut hemisphere symmetrically against to the X-O-Y plane.
Integration intervals
- φ angle interval is constant:
Where a is the cut angle in radians
and(3)
- Radius integration interval
The radius upper bound is limited by sphere surface - R. Cutting plane limits the lower radius bound, according (1)
(4)
- θ angle intervals
We'll integrate only over upper half of θ interval, so upper limit of θ isand lower limit equation can be evaluated from (1) with r=R in this way:
(5)
Or using (3) we can write it like this:
(6)
Volume formula
To obtain Volume formula for hemisphere cut we solve integral (2) using intervals (3),(4),(6):
-
Integrate over r
Result:
-
Integrate over θ
Result:
- Integrate over φ
So the final volume formula is:
where:
,
.
Comments